Bayes. Mediation. Lots of data.
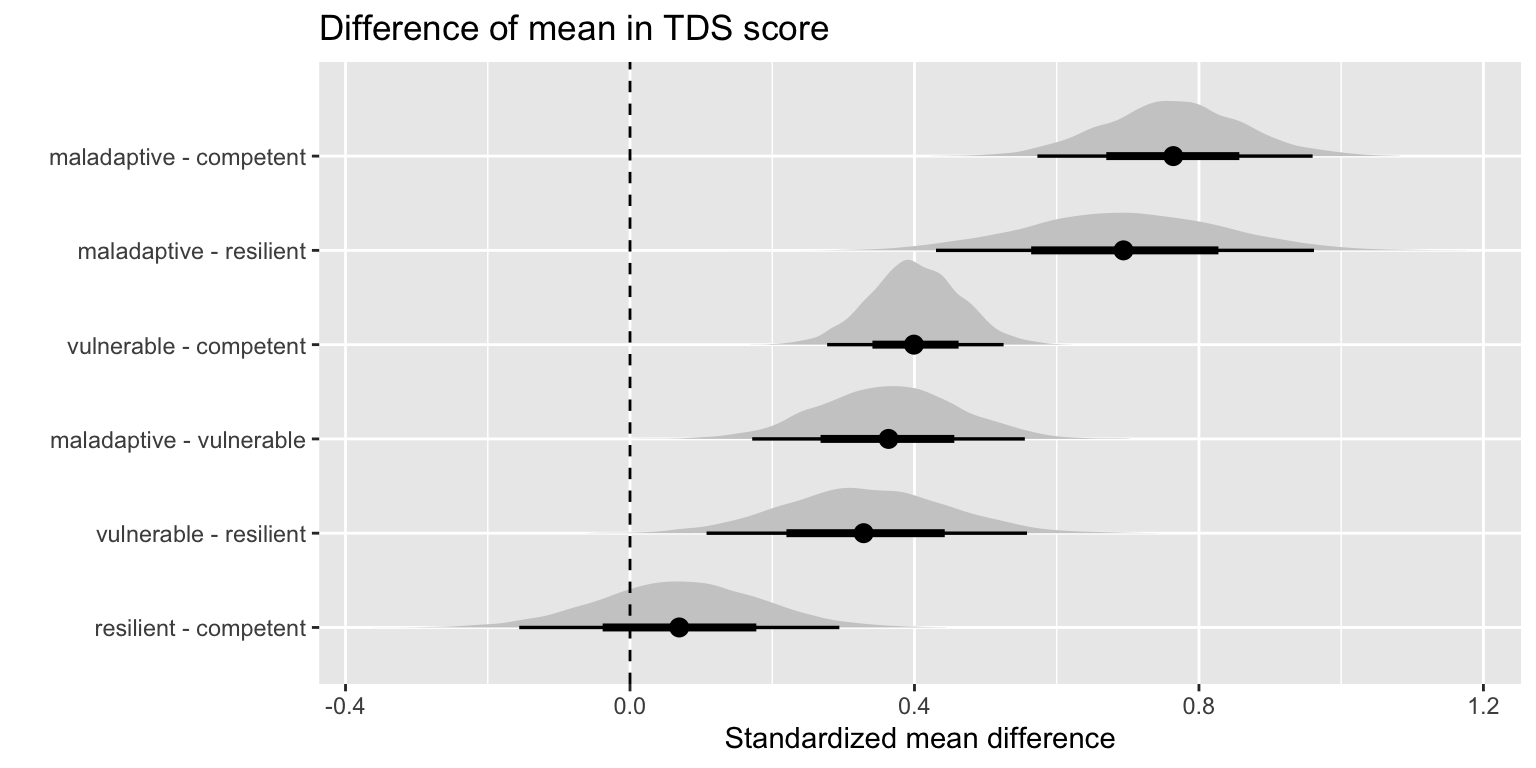
In this study I use data from the IMAGEN Study (initial n=2315) to determine if mental health and drug use in adulthood (~age 23) can be predicted by resilience in early adolescence (~age 14). Adolescents are classified into one of four groups following Burt et al’s operationalization of resilience as the interaction between competence and adversity. In addition, I look at whether structural brain differences at age 14 in brain regions identified by Burt mediate any of the differences observed in mental health outcomes and alcohol use at age 23.
To summarize, I find that there are significant differences in mental health outcomes and recent drug use at age 23 between the four groups. Additionally, the gray matter volume differences identified between the groups at age 14 did not mediate any of the differences in mental health or drug use. These results suggest that developmental features of early resilience such as social skills interact with adversity in a positive way and are predictive of numerous outcomes in adulthood. This corroborates with findings by (Roisman et al. 2004) that suggest the importance of developmentally salient tasks in predicting adult success.
Resilience: The capacity of a dynamic system to withstand or recover from significant challenges that threaten its stability, viability, or development.
Resilience refers to the phenomenon of positive adaptation in the face of adverse life experiences (Masten 2011). Individuals who have had adverse life experiences are at higher risk of developing problems with mental health and drug use (Fritz et al. 2020). However the effects of adversity are varied. Some individuals have better outcomes than others despite experiencing similar levels of adversity. The study of resilience is thus concerned with understanding the factors and mechanisms that explain the variability of outcomes in people who have experienced significant adversity.
In this study I follow up on results produced by (Burt et al. 2016) using data from the IMAGEN Study. Burt et al. defined resilience in terms of the interaction between two binarized variables competence and adversity (details to follow further below). This yielded four groups into which participants were classified. Using this classification scheme, they discovered structural brain differences in four brain regions across the groups. One of these regions (right middle frontal gyrus) was found to be negatively correlated with a drinking composite score, suggesting that greater gray matter volume in this region may be protective of problematic alcohol use.
The IMAGEN Study has since collected follow-up data at three subsequent time points. These data include various measures of mental health and drug use, among others. Here I use the same classification schema as Burt et al to assess whether these groups defined at age 14 are predictive of mental health and drug use behavior 9 years later. Additionally, I test whether or not these potential differences in outcomes are mediated by the structural brain differences reported by Burt et al. My apriori guesses (hypotheses) are that differences in mental health will be better predicted than differences in drug use, and that the brain regions identified by Burt et al will play no role in mediating these differences.
library(tidyverse)
library(datawizard)
library(brms)
library(vroom)
library(corrr)
library(gtsummary)
library(marginaleffects)
library(tidybayes)
options(brms.backend = "cmdstanr")
options(stan_model_args=list(stanc_options = list("O1")))
options(mc.cores = 4)
set.seed(5)d <- vroom("~/Desktop/PhD/resilience-im-burt/resil_grouped_data.csv") |>
mutate(class = factor(class,
levels = c("competent",
"resilient",
"vulnerable",
"maladaptive")),
pds_cat = factor(pds_cat),
sex = factor(sex),
recruitment_centre = factor(recruitment_centre),
all_handedness = factor(all_handedness),
# mean center continuous covariates
pds_sum_c = center(pds_sum),
v_iq_c = center(v_iq),
p_iq_c = center(p_iq),
age_years_bsl_c = center(age_years_bsl),
# for ordered probit
across(contains("alcohol"), ~ factor(.x, ordered = T, exclude = NA)),
across(contains("mj_hash_"), ~ factor(.x, ordered = T, exclude = NA)),
across(contains("cigs_"), ~ factor(.x, ordered = T, exclude = NA)),
across(`8a_bsl`:`21_bsl`, ~ factor(.x, ordered = T, exclude = NA)),
across(`8a_fu1`:`21_fu1`, ~ factor(.x, ordered = T, exclude = NA)),
across(`8a_fu2`:`21_fu2`, ~ factor(.x, ordered = T, exclude = NA)),
across(`8a_fu3`:`21_fu3`, ~ factor(.x, ordered = T, exclude = NA)),
sex = case_when(sex == 1 ~ "Male",
sex == 2 ~ "Female"),
all_handedness = case_when(all_handedness == 0 ~ "Left",
all_handedness == 1 ~ "Right"),
# standardize sum score outcomes
audit_total_score_fu3 = standardize(audit_total_score_fu3),
cesd_c_sum_fu3 = standardize(cesd_c_sum_fu3),
dawba_sdq_c_sebdtot_fu3 = standardize(dawba_sdq_c_sebdtot_fu3),
externalizing_fu3 = standardize(externalizing_fu3),
internalizing_fu3 = standardize(internalizing_fu3),
pss_c_sum_fu3 = standardize(pss_c_sum_fu3),
rapi_c_sum_fu3 = standardize(rapi_c_sum_fu3)
)z_score <- function(x, miss_rmv = F){
(x - mean(x, na.rm = miss_rmv)) / sd(x, na.rm = miss_rmv)
}
pomp <- function(obs, min, max){
((obs-min)/(max-min)) * 100
}
contrast_plot <- function(model,
contrast_type = "",
rope = NA,
rope_pomp,
pomp = F,
pomp_min = NA,
pomp_max = NA,
scale = "",
newdata = "mean",
contrasts_df = F
){
# compute class contrasts and gather draws
contrasts_hdi <- model |>
comparisons(variables = list(class = "pairwise"),
# compute adjusted comparisons where covariates are held at their average value (cont)
newdata = newdata) |>
mutate(pomp_diff = pomp(comparison, pomp_min, pomp_max),
pomp.low = pomp(conf.low, pomp_min, pomp_max),
pomp.high = pomp(conf.high, pomp_min, pomp_max),
across(where(is.numeric), ~round(.x, 2))) |>
select(contrast, comparison, conf.low, conf.high, pomp_diff, pomp.low, pomp.high) |>
arrange(desc(comparison))
contrast_draws <- model |>
comparisons(variables = list(class = "pairwise"),
newdata = newdata) |>
posteriordraws()
plot_raw <- contrast_draws |>
ggplot(aes(x = draw,
y = fct_reorder(contrast, draw, mean),
fill = stat(abs(x) > rope))) +
stat_halfeye() +
labs(x = "Standardized mean difference",
y = "",
title = str_c("Difference of ", contrast_type, " in ", scale, " score")) +
geom_vline(xintercept = c(-rope, rope), linetype = "dashed") +
scale_fill_manual(values = c("gray80", "skyblue")) +
theme(legend.position="none")
if (pomp == T){
plot_pomp <- contrast_draws |>
mutate(pomp = pomp(draw, pomp_min, pomp_max)) |>
ggplot(aes(x = pomp,
y = fct_reorder(contrast, pomp, mean),
fill = stat(abs(x) > rope_pomp))) +
stat_halfeye() +
labs(x = "Percent of maximum possible (POMP)",
y = "",
title = str_c("Difference of POMP in ", scale, " score")) +
geom_vline(xintercept = c(-rope_pomp, rope_pomp), linetype = "dashed") +
scale_fill_manual(values = c("gray80", "skyblue")) +
theme(legend.position="none")
} else {
plot_pomp = NULL
}
if (contrasts_df == T) {
list(
contrasts_df = contrast_draws,
contrasts_hdi = contrasts_hdi,
plot_raw = plot_raw,
plot_pomp = plot_pomp
)
} else {
list(
contrasts_df = NULL,
contrasts_hdi = contrasts_hdi,
plot_raw = plot_raw,
plot_pomp = plot_pomp
)
}
}
qi_table <- function(fit){
fit |>
as_draws_df() |>
select(contains("b_")) |>
pivot_longer(cols=everything()) |>
group_by(name) |>
tidybayes::mean_qi() |>
select(name, value, .lower, .upper) |>
mutate(across(where(is.numeric), ~round(., 2))) |>
rmarkdown::paged_table()
}
coef_plot <- function(fit, title){
fit |>
as_draws_df() |>
select(contains("b_")) |>
pivot_longer(cols=everything()) |>
ggplot(aes(y=name, x = value)) +
stat_halfeye() +
geom_vline(xintercept = 0, linetype = "dashed") +
labs(x = "Coefficient value", y = "", title = title)
}The IMAGEN dataset was obtained from eight sites in Europe: Berlin, Dresden, Dublin, Hamburg, London, Mannheim, Nottingham, and Paris. Adolescent participants completed a series of self-report and interview measures, in addition to structural MRI scans. Parent-reported data were also obtained for some measures. Data were collected at four time points: baseline, follow-up 1, follow-up 2, follow-up 3. Additional information on the sample and data acquisition can be found on the IMAGEN website and from Schumann et al.
d |>
select(age_years_bsl,
sex,
recruitment_centre
) |>
tbl_summary(by = recruitment_centre,
label = list(age_years_bsl = "Age (years)",
sex = "Sex",
recruitment_centre = "Study site"),
missing_text = "Missing", digits = everything() ~ 1) |>
modify_header(label ~ "Variable") |>
bold_labels() |>
modify_spanning_header("stat_1":"stat_8" ~ "**Study Site**") |>
modify_caption("**Table 1. Baseline Demographics Table**") |>
as_gt()| Variable | Study Site | |||||||
|---|---|---|---|---|---|---|---|---|
| 1, N = 3751 | 2, N = 2821 | 3, N = 2741 | 4, N = 2831 | 5, N = 2671 | 6, N = 2851 | 7, N = 2911 | 8, N = 2581 | |
| Age (years) | 14.5 (14.2, 14.7) | 14.7 (14.3, 14.9) | 14.4 (14.0, 14.8) | 14.5 (14.2, 14.7) | 14.3 (14.0, 14.6) | 14.3 (14.0, 14.6) | 14.5 (14.1, 14.8) | 14.4 (14.1, 14.6) |
| Missing | 26 | 21 | 13 | 25 | 5 | 28 | 33 | 48 |
| Sex | ||||||||
| Female | 180.0 (48.0%) | 133.0 (47.2%) | 136.0 (49.6%) | 148.0 (52.3%) | 145.0 (54.3%) | 152.0 (53.3%) | 161.0 (55.3%) | 122.0 (47.3%) |
| Male | 195.0 (52.0%) | 149.0 (52.8%) | 138.0 (50.4%) | 135.0 (47.7%) | 122.0 (45.7%) | 133.0 (46.7%) | 130.0 (44.7%) | 136.0 (52.7%) |
| 1 Median (IQR); n (%) | ||||||||
Adversity is operationalized and drawn from the Life-Events Questionnaire, which uses 39 items to measure the lifetime occurrence of stressful life events across seven domains: family/parents, accident/illness, sexuality, autonomy, deviance, relocation, and distress. Additionally each item has a corresponding valence or perceived desirability of the event measured on a five-point Likert scale with responses: Very unhappy, Unhappy, Neutral, Happy, Very happy.
Competence is operationalized as the sum of standardized scores across four domains:
Rule-abiding conduct (40 items): 15 self- and parent-reported dichotomized DAWBA items assessing rule-breaking behavior in the past year as well as 5 self- and parent-reported SDQ items. (reverse-scored, once aggregated, such that higher scores represented greater rule-abiding conduct).
Social competence (41 items). 10 self- and 11 parent-reported DAWBA items representing prosocial behavior (each scored on a 0-2 scale) as well as 10 self- and 10 parent-reported SDQ items representing the Peer Problems (reversed) and Prosocial Behavior subscales.
Academic competence (4 items): 2 parent-reported DAWBA items (0-2 scale: “good at school work”; “general reasoning and school work”), 1 self-reported DAWBA item (0-2 scale: “good at school work”) and 1 ESPAD item (8-point scale representing ‘A’ to ‘C-’).
Emotional health (10 items): 5 self- and 5 parent-reported (all reversed) SDQ Emotional Symptoms items.
Standardized scores were calculated by aggregating items within each domain and computing a z-score. Scores beyond 3 standard deviations from the mean were truncated. Z-scores were then summed across domain, yielding a final competence score.
Following Burt et al, participants are classified into one of four groups based on where they fall along the competence and adversity measures.
First, competence was binarized based on whether participants had a z-score higher or lower than \(-0.5\) on all four competence domains. According to (Burt et al. 2016), this represents “a stringent definition of ‘doing well’ as it encompasses not only meeting external developmental task criteria (Roisman et al. 2004) but also non-elevated emotional symptoms.”
Second, adversity was also binarized based on a cutoff value of \(1\) standard deviation on number of negative lifetime events. This represents 6 or more events.
Crossing these binarized variables yielded four possible group classifications:
(C/a): High competence, low adversity (sometimes termed ‘competent’)
(C/A) High competence, high adversity (‘resilient’)
(c/a) Low competence, low adversity (‘vulnerable’)
(c/A) Low competence, high adversity (‘maladaptive’)
Participants were required to have non-missing data for at least one competence indicator to receive a competence composite in some form, yielding \(n=2107\) classified subjects.
| N = 2,3151 | |
|---|---|
| class | |
| competent | 740 (35%) |
| resilient | 146 (6.9%) |
| vulnerable | 964 (46%) |
| maladaptive | 257 (12%) |
| Unknown | 208 |
| 1 n (%) | |
While competence/adversity groupings were constructed at baseline (around age 14), the outcome measures of this study were obtained at the third follow-up point of the study (around age 23).
The SDQ (Goodman, 1997) is a 25-item questionnaire completed by both adolescents and parents in the current study. It is divided into five subscales: emotional symptoms, conduct problems, hyperactivity/inattention, peer relationship problems, and prosocial behaviors. Each item is scored on a three-point scale (0 = not true, 1 = somewhat true, 2 = certainly true).
From the SDQ I use the Total Difficulty score as a measure of mental health. The total problem score is generated by summing the scores for all the scales except the prosocial scale. The resulting score ranges from \(0–40\). Each scale has five items, and there are four scales. The total score was not calculated if one of the component scores was missing.
Additionally, I decomposed the Total Difficulty Score into an Internalizing score and an Externalizing score to examine mental health problems in a more specific way. This aligns with how psychopathology is widely conceptualized such as in the ACEBA. Internalizing simply corresponds to the sum of items across the Emotional Symptoms scale and the Peer Relationship Problems scale in the SDQ. Externalizing corresponds to the sum of items across the Conduct Problems scale and the Hyperactivity/Inattention scale in the SDQ.
The CESD consists of twenty items that are rated on a four-poing likert scale (from 1: rarely or none of the time to 4: most or all of the time). Scores range from zero to sixty. Higher scores indicated a higher frequency of depressive symptoms during the last week.
Since some of the items from the SDQ are used in constructing competence, I use the sum score from the CESD as another measure of mental health to account for the expected differences in the Total Difficulty score.
The Perceived Stress Scale is a 10-item self report questionnaire that measures persons’ evaluation of the stressfulness of the situations in the past month of their lives. There is also a 4-item version. Scores can range from 0 to 40, with higher scores indicating greater stress.
The AUDIT has 10 questions and the possible responses to each question are scored 0, 1, 2, 3 or 4, with the exception of questions 9 and 10 which have possible responses of 0, 2 and 4.
The range of possible scores is from 0 to 40 where 0 indicates an abstainer who has never had any problems from alcohol. A score of 1 to 7 suggests low-risk consumption according to World Health Organization (WHO) guidelines. Scores from 8 to 14 suggest hazardous or harmful alcohol consumption and a score of 15 or more indicates the likelihood of alcohol dependence (moderate-severe alcohol use disorder).
The RAPI is a 23-item self-administered screening tool for assessing adolescent problem drinking. It was developed in order to create a conceptually sound, unidimensional, relatively brief, and easily administered instrument to assess problem drinking in adolescence. The advantages of this screening tool lie in its ease of administration and its standardization, which make it possible to compare problem drinking scores across groups.
The ESPAD (Hibell et al., 1997) was administered using the computerized assessment platform Psytools (Delosis, London, UK). Psytools presented questionnaire items and response alternatives on a computer screen, with jump rules to skip inapplicable questions for the sake of brevity. As the Psytools program was run at the participant’s home without direct supervision by the research team, the reliability of individual data was checked in a two-stage procedure. Before every task, adolescents were asked to report on the current testing context including questions about their attentional focus and the confidentiality of the setting. Automated flags highlighted potentially problematic testing situations and were followed up by research assistants in confidential face-to-face sessions. Final reliability ratings were assigned which led to exclusion of the data in certain cases. Specifically, exclusion criteria for substance use measures included an indication that the participant was in a hurry, somebody was watching, or an indication of having known of or taken the sham drug Relevin.
To assess cigarette and marijuana/hash use, I gather two variables from the ESPAD that correspond to frequency of cigarette and marijuana/hash use within the past 30 days. Each item has seven response categories:
How frequently have you smoked cigarettes during the LAST 30 DAYS?
0 - “Not at all”
1 - “Less than one cigarette a week”
2 - “Less than one cigarette per day”
3 - “1-5 cigarettes per day”
4 - “6-10 cigarettes per day”
5 - “11-20 cigarettes per day”
6 - “More than 20 cigarettes per day”
On how many occasions OVER THE LAST 30 DAYS have you used marijuana (grass, pot) or hashish (hash, hash oil)?
0 - “0”
1 - “1-2”
2 - “3-5”
3 - “6-9”
4 - “10-19”
5 - “20-39”
6 - “40 or more”
All analyses were conducted in R (version 4.2.1) and primarily employ a Bayesian framework. The benefits of using a Bayesian approach have been highlighted extensively elsewhere (Dienes 2011; Kruschke 2013; van de Schoot et al. 2014). Prior to model fitting, continuous covariates were mean-centered, continuous* outcomes were standardized, and categorical variables were left as is. Missing values were dropped during model fitting (case-dropping).
*Sum scores are technically not continuous, but are often treated as such. I will follow suit for ease and simplicity.
For predicting mental health and drug use in adulthood, I use seven outcomes:
Each outcome is regressed onto class (the competence/adversity groupings), in addition to a set of covariates to statistically control for possible confounding effects. The set of covariates correspond to measurements at baseline. The included covariates are:
To account for the effect of outliers without excluding them entirely, I use a Student-t distribution as the likelihood (see Robust linear regression) for modeling first five outcomes: TDS, CESD, PSS, AUD, and RAP. As noted by (McElreath 2020), the model will still produce similar coefficient estimates to a regression model using a Gaussian likelihood, but is more robust to the presence of outliers. For MJH and CIG, I use the ordered probit to properly model each item as Likert-scale responses.
Priors for each model are weakly informative, thus allowing the data “to speak” and inform coefficient estimates. In general, for the first five outcomes, the mathematical description looks like
\[ \begin{gather} \text{outcome}_i \sim \text{Student-t}(\nu, \mu_i, \sigma^{2}) \\ \mu_i = \beta_{0} + \sum_{j=1}^{p}\beta_{j}X_{j} \\ \beta_{0}, \beta_{j} \sim \text{Normal}(0,10) \\ \sigma \sim \text{Exponential}(0.5)\\ \nu \sim \text{gamma}(2, 0.1) \\ \end{gather} \]where \(i\) indexes each participant. This also allows for Bayesian hypothesis testing, which will be detailed in each analysis section.
For the ordered probit models, the mathematical description is slightly different. We instead have
\[ \begin{gather} p(\text{response} = k \mid \{\tau_k\}, \mu_i) = \Phi(\tau_{k} - \mu_i) - \Phi(\tau_{k-1} - \mu_i) \\ \mu_i = \sum_{j=1}^{p}\beta_{j}X_{j} \\ \tau_{0-6} \sim \text{Normal}(0, 3)\\ \beta_{j} \sim \text{Normal}(0,10) \end{gather} \]where we have \(k+1\) possible responses to an item (e.g. \(k=6\) “How frequently have you smoked cigarettes during the last 30 days?”). \(\Phi\) denotes the cumulative distribution function for a standard normal distribution (mean: \(0\), sd: \(1\)), and \(\tau_{0-6}\) represents the threshold values that divide the standard normal distribution into regions that correspond to the probability of each response\(k\). More on the ordered probit model is discussed in (Bürkner and Vuorre 2019) and (McElreath 2020).
For each sum score outcome, I will 1) fit the model 2) display a table containing the 95% CI and posterior point estimate for each coefficient 3) plot the posterior distribution of coefficient estimates, and 4) plot a contrast plot between each competence/adversity group, which represents the standardized difference in means between each group. For the ordinal variables (frequency of cigarette and mj/hash use) I include 1-3 but no contrast plot.
Okay, let’s get modeling!
A preview of the data I used for analysis.
d |>
select(id, class,
sex, recruitment_centre, all_handedness,
pds_sum_c, v_iq_c, p_iq_c, age_years_bsl_c,
audit_total_score_fu3,
dawba_sdq_c_sebdtot_fu3,
externalizing_fu3,
internalizing_fu3,
pss_c_sum_fu3,
rapi_c_sum_fu3,
cigs_frequency_past_30_days_fu3,
mj_hash_past_30_days_fu3
) |>
head() |>
rmarkdown::paged_table()m_tds <- brm(
formula = dawba_sdq_c_sebdtot_fu3 ~ 1 + class + sex + pds_sum_c + v_iq_c + p_iq_c + age_years_bsl_c + recruitment_centre + all_handedness,
prior = c(
prior(normal(0, 10), class = Intercept),
prior(normal(0, 10), class = b),
prior(gamma(2, 0.1), class = nu),
prior(exponential(0.5), class = sigma)
),
sample_prior = "yes",
data = d,
family = student,
iter = 2000,
warmup = 500,
chains = 4,
seed = 5,
# file_refit = "on_change",
file = "~/Desktop/PhD/resilience-im-burt/brms-fits/m2_tds_student_cov"
)qi_table(m_tds)coef_plot(m_tds, "TDS")
tds_contrast <- contrast_plot(
model = m_tds,
contrast_type = "mean",
rope = 0,
pomp_min = 0,
pomp_max = 40,
rope_pomp = 2.5,
pomp = F,
scale = "TDS")
tds_contrast$plot_raw
m_int <- brm(
formula = internalizing_fu3 ~ 1 + class + sex + pds_sum_c + v_iq_c + p_iq_c + age_years_bsl_c + recruitment_centre + all_handedness,
prior = c(
prior(normal(0, 10), class = Intercept),
prior(normal(0, 10), class = b),
prior(gamma(2, 0.1), class = nu),
prior(exponential(0.5), class = sigma)
),
sample_prior = "yes",
data = d,
family = student,
iter = 2000,
warmup = 500,
chains = 4,
seed = 5,
# file_refit = "on_change",
file = "~/Desktop/PhD/resilience-im-burt/brms-fits/m2_internalizing"
)qi_table(m_int)coef_plot(m_int, "Internalizing score")
int_contrast <- contrast_plot(
model = m_int,
contrast_type = "mean",
rope = 0,
pomp = F,
scale = "Internalizing")
int_contrast$plot_raw
m_ext <- brm(
formula = externalizing_fu3 ~ 1 + class + sex + pds_sum_c + v_iq_c + p_iq_c + age_years_bsl_c + recruitment_centre + all_handedness,
prior = c(
prior(normal(0, 10), class = Intercept),
prior(normal(0, 10), class = b),
prior(gamma(2, 0.1), class = nu),
prior(exponential(0.5), class = sigma)
),
sample_prior = "yes",
data = d,
family = student,
iter = 2000,
warmup = 500,
chains = 4,
seed = 5,
# file_refit = "on_change",
file = "~/Desktop/PhD/resilience-im-burt/brms-fits/m2_externalizing"
)qi_table(m_ext)coef_plot(m_ext, "Externalizing")
ext_contrast <- contrast_plot(
model = m_ext,
contrast_type = "mean",
rope = 0,
pomp_min = 0,
pomp_max = 40,
rope_pomp = 2.5,
pomp = F,
scale = "Externalizing")
ext_contrast$plot_raw
m_cesd <- brm(
formula = cesd_c_sum_fu3 ~ 1 + class + sex + pds_sum_c + v_iq_c + p_iq_c + age_years_bsl_c + recruitment_centre +
all_handedness,
data = d,
prior = c(
prior(student_t(3, 5, 4.4), class = Intercept),
prior(normal(0, 10), class = b),
prior(gamma(2, 0.1), class = nu),
prior(exponential(0.5), class = sigma)
),
family = student,
iter = 2000,
warmup = 500,
chains = 4,
seed = 5,
sample_prior = "yes",
# file_refit = "on_change",
file = "~/Desktop/PhD/resilience-im-burt/brms-fits/m2_cesd_student"
)qi_table(m_cesd)coef_plot(m_cesd, "CESD")
cesd_contrast <- contrast_plot(
model = m_int,
contrast_type = "mean",
rope = 0,
pomp = F,
scale = "CESD")
cesd_contrast$plot_raw
m_audit_sum <- brm(
audit_total_score_fu3 ~ 1 + class + sex + pds_sum_c + v_iq_c + p_iq_c + age_years_bsl_c + recruitment_centre +
all_handedness,
data = d,
family = student,
prior = c(
prior(student_t(3, 5, 4.4), class = Intercept),
prior(normal(0, 5), class = b),
prior(gamma(2, 0.1), class = nu),
prior(exponential(0.5), class = sigma)
),
iter = 2000,
warmup = 500,
chains = 4,
seed = 5,
sample_prior = "yes",
file = "~/Desktop/PhD/resilience-im-burt/brms-fits/m2_audit_total_cov"
)qi_table(m_audit_sum)coef_plot(m_audit_sum, "AUDIT")
aud_contrast <- contrast_plot(
model = m_audit_sum,
contrast_type = "mean",
rope = 0,
pomp_min = 0,
pomp_max = 40,
rope_pomp = 2.5,
pomp = F,
scale = "AUDIT")
aud_contrast$plot_raw
m_rapi <- brm(
rapi_c_sum_fu3 ~ 1 + class + sex + pds_sum_c + v_iq_c + p_iq_c + age_years_bsl_c + recruitment_centre +
all_handedness,
data = d,
family = student,
prior = c(
prior(student_t(3, 5, 4.4), class = Intercept),
prior(normal(0, 5), class = b),
prior(gamma(2, 0.1), class = nu),
prior(exponential(0.5), class = sigma)
),
iter = 2000,
warmup = 500,
chains = 4,
seed = 5,
# file_refit = "on_change",
sample_prior = "yes",
file = "~/Desktop/PhD/resilience-im-burt/brms-fits/m2_rapi_cov"
)qi_table(m_rapi)coef_plot(m_rapi, "RAPI")
rapi_contrast <- contrast_plot(
model = m_rapi,
contrast_type = "mean",
rope = 0,
pomp = F,
scale = "RAPI")
rapi_contrast$plot_raw
m_pss <- brm(
pss_c_sum_fu3 ~ 1 + class + sex + pds_sum_c + v_iq_c + p_iq_c + age_years_bsl_c + recruitment_centre +
all_handedness,
data = d,
family = student,
prior = c(
prior(student_t(3, 5, 4.4), class = Intercept),
prior(normal(0, 10), class = b),
prior(gamma(2, 0.1), class = nu),
prior(exponential(0.5), class = sigma)
),
iter = 2000,
warmup = 500,
chains = 4,
seed = 5,
# file_refit = "on_change",
sample_prior = "yes",
file = "~/Desktop/PhD/resilience-im-burt/brms-fits/m2_pss_cov"
)qi_table(m_pss)coef_plot(m_ext, "PSS")
pss_contrast <- contrast_plot(
model = m_pss,
contrast_type = "mean",
rope = 0,
pomp = F,
scale = "PSS")
pss_contrast$plot_raw
m_cig <- brm(
formula = cigs_frequency_past_30_days_fu3 ~ 1 + class + pds_sum_c + v_iq_c + p_iq_c + age_years_bsl_c + recruitment_centre + all_handedness,
data = d,
family = cumulative(probit),
prior = c(
prior(normal(0, 2), class = Intercept),
prior(normal(0, 1), class = b)
),
warmup = 500,
iter = 3000,
chains = 4,
seed = 5,
init = 0.2,
control = list(adapt_delta = .99),
sample_prior = "yes",
# file_refit = "on_change",
file = "~/Desktop/PhD/resilience-im-burt/brms-fits/b2_cig_freq"
)qi_table(m_cig)coef_plot(m_cig, "Cigarette Frequency")
For the predicted responses, we generate a number of responses for individuals within each resilience group, repeated several thousand times, i.e. for each draw from the MCMC chain, we will generate a number of predicted responses for each group. What we could look at to determine if groups are different is the contrast in the expected value of responses.
m_mj <- brm(
formula = mj_hash_past_30_days_fu3 ~ 1 + class + pds_sum_c + v_iq_c + p_iq_c + age_years_bsl_c + recruitment_centre
+ all_handedness,
data = d,
family = cumulative(probit),
prior = c(prior(normal(0, 2), class = Intercept),
prior(normal(0, 1), class = b)),
iter = 3000,
warmup = 500,
chains = 4,
seed = 5,
init = 0.2,
sample_prior = "yes",
# file_refit = "on_change",
control = list(adapt_delta = .99),
file = "~/Desktop/PhD/resilience-im-burt/brms-fits/m_mj_hash"
)qi_table(m_mj)coef_plot(m_mj, "Marijuana Use Frequency")
For the predicted responses, we generate a number of responses for individuals within each resilience group, repeated several thousand times, i.e. for each draw from the MCMC chain, we will generate a number of predicted responses for each group. What we could look at to determine if groups are different is the contrast in the expected value of responses.
For each of the sum score outcomes above, I run a mediation analysis using as mediators the structural brain differences Burt et al identified. In other words, I want to know if these brain differences mediate any of the effects of the competence/adversity groupings on mental health or drug use.
Once the models are fit, I compute posterior distributions over the direct and indirect effects. Given these distributions, I then conduct a Bayesian hypothesis test (Wagenmakers et al. 2010) to examine if there are substantial mediation effects in any of the regions. In short the test computes a ratio of the posterior density and prior density at a specified value of the effect of interest. Below I specify the value at \(0\) as an analogue to null hypothesis significance testing. An additional benefit of this test is that it also gives evidence for the null rather than only evidence against it.
hyp <- function(outcome, model){
outcome <- str_remove_all(outcome, "_")
hyp_v <- c(
str_c("cl204440MEadv_classresilient", "*", outcome, "_cl20_44_40_ME_adv", "=0"),
str_c("cl204440MEadv_classvulnerable", "*", outcome, "_cl20_44_40_ME_adv", "=0"),
str_c("cl204440MEadv_classmaladaptive", "*", outcome, "_cl20_44_40_ME_adv", "=0"),
str_c("cl141470AdvXComp_classresilient", "*", outcome, "_cl14_14_70_AdvXComp", "=0"),
str_c("cl141470AdvXComp_classvulnerable", "*", outcome, "_cl14_14_70_AdvXComp", "=0"),
str_c("cl141470AdvXComp_classmaladaptive", "*", outcome, "_cl14_14_70_AdvXComp", "=0"),
str_c("cl324427MEAdv_classresilient", "*", outcome, "_cl32_44_27_ME_Adv", "=0"),
str_c("cl324427MEAdv_classvulnerable", "*", outcome, "_cl32_44_27_ME_Adv", "=0"),
str_c("cl324427MEAdv_classmaladaptive", "*", outcome, "_cl32_44_27_ME_Adv", "=0"),
str_c("cl324521AdvXComp_classresilient", "*", outcome, "_cl32_45_21_AdvXComp", "=0"),
str_c("cl324521AdvXComp_classvulnerable", "*", outcome, "_cl32_45_21_AdvXComp", "=0"),
str_c("cl324521AdvXComp_classmaladaptive", "*", outcome, "_cl32_45_21_AdvXComp", "=0"),
str_c("clm636m21MEComp_classresilient", "*", outcome, "_clm6_36_m21_ME_Comp", "=0"),
str_c("clm636m21MEComp_classvulnerable", "*", outcome, "_clm6_36_m21_ME_Comp", "=0"),
str_c("clm636m21MEComp_classmaladaptive", "*", outcome, "_clm6_36_m21_ME_Comp", "=0")
)
fit <- hypothesis(model, hyp_v)
fit
}I also plot the posterior distributions of the indirect effect of each class, following the recommendations of (Hayes and Preacher 2014).
med_tds <- brm(
formula = bf(dawba_sdq_c_sebdtot_fu3 ~ class + sex +
cl14_14_70_AdvXComp + cl20_44_40_ME_adv +
cl32_44_27_ME_Adv + cl32_45_21_AdvXComp +
clm6_36_m21_ME_Comp + pds_sum_c +
v_iq_c + p_iq_c + age_years_bsl_c +
recruitment_centre + all_handedness) +
m1 + m2 + m3 + m4 + m5,
data = d,
sample_prior = "yes",
# file_refit = "on_change",
prior = c(prior(normal(0, 3), class = Intercept),
prior(normal(0, 5), class = b)),
iter = 2500,
warmup = 500,
chains = 4,
seed = 5,
file = "~/Desktop/PhD/resilience-im-burt/brms-fits/mediation_tds"
)
hyp_tds <- hyp("dawba_sdq_c_sebdtot_fu3", med_tds)
hyp_tds$hypothesis |>
select(Evid.Ratio, Estimate, Est.Error, contains("CI"), Hypothesis) |>
mutate(across(where(is.numeric), ~round(., 3))) |>
rmarkdown::paged_table()Table of Bayesian hypothesis test results. (Evidence ratio > 1 supports “null” hypothesis. Evidence ratio < 1 supports “alternative” hypothesis.) Each row represents a different indirect effect for each unique pair of class and brain region.
Plotted below are the posteriors of the indirect effect.
med_tds |>
as_draws_df() |>
select(.draw,
contains("_class"),
contains("b_dawbasdqcsebdtotfu3_c")) |>
pivot_longer(cols = matches("(b_cl.*)_(class.*)"),
names_to = c("mediator_a", "class"),
names_pattern = "(b_cl.*)_(class.*)",
values_to = "a") |>
pivot_longer(cols = matches("(b_dawbasdqcsebdtotfu3)_(cl..)_(.*)"),
names_to = c("outcome", "mediator_b"),
names_pattern = "(b_dawbasdqcsebdtotfu3)_(cl.*)",
values_to = "b") |>
# compute ab for every class, for every brain mediator
mutate(ab = a * b,
mediator_a = str_remove(mediator_a, "b_"),
mediator_b = str_remove_all(mediator_a, "_"),
mediator = mediator_a == mediator_b) |>
#group_by(mediator_a) |>
#mean_qi(ab) |>
# mutate(across(where(is.numeric), ~round(.x, 3)))
ggplot(aes(x = ab, y = mediator_a)) +
stat_halfeye() +
xlim(-0.3, 0.3) +
labs(y = "", x = "a * b")
med_cesd <- brm(
formula = bf(cesd_c_sum_fu3 ~ class + sex +
cl14_14_70_AdvXComp + cl20_44_40_ME_adv +
cl32_44_27_ME_Adv + cl32_45_21_AdvXComp +
clm6_36_m21_ME_Comp +
pds_sum_c + v_iq_c + p_iq_c +
age_years_bsl_c + recruitment_centre + all_handedness) +
m1 + m2 + m3 + m4 + m5,
data = d,
sample_prior = "yes",
# file_refit = "on_change",
prior = c(prior(normal(0, 3), class = Intercept),
prior(normal(0, 5), class = b)),
iter = 2500,
warmup = 500,
chains = 4,
seed = 5,
file = "~/Desktop/PhD/resilience-im-burt/brms-fits/mediation_cesd"
)
hyp_cesd <- hyp("cesd_c_sum_fu3", med_cesd)
hyp_cesd$hypothesis |>
select(Evid.Ratio, Estimate, Est.Error, contains("CI"), Hypothesis) |>
mutate(across(where(is.numeric), ~round(., 3))) |>
rmarkdown::paged_table()Table of Bayesian hypothesis test results. (Evidence ratio > 1 supports “null” hypothesis. Evidence ratio < 1 supports “alternative” hypothesis.) Each row represents a different indirect effect for each unique pair of class and brain region.
Plotted below are the posteriors of the indirect effect.
med_cesd |>
as_draws_df() |>
select(.draw,
contains("_class"),
contains("b_cesdcsumfu3_c")) |>
pivot_longer(cols = matches("(b_cl.*)_(class.*)"),
names_to = c("mediator_a", "class"),
names_pattern = "(b_cl.*)_(class.*)",
values_to = "a") |>
pivot_longer(cols = matches("(b_cesdcsumfu3)_(cl..)_(.*)"),
names_to = c("outcome", "mediator_b"),
names_pattern = "(b_cesdcsumfu3)_(cl.*)",
values_to = "b") |>
# compute ab for every class, for every brain mediator
mutate(ab = a * b,
mediator_a = str_remove(mediator_a, "b_"),
mediator_b = str_remove_all(mediator_a, "_"),
mediator = mediator_a == mediator_b) |>
#group_by(mediator_a) |>
#mean_qi(ab) |>
# mutate(across(where(is.numeric), ~round(.x, 3)))
ggplot(aes(x = ab, y = mediator_a)) +
stat_halfeye() +
xlim(-0.3, 0.3) +
labs(y = "", x = "a * b")
med_aud <- brm(
formula = bf(audit_total_score_fu3 ~ class + sex +
cl14_14_70_AdvXComp + cl20_44_40_ME_adv +
cl32_44_27_ME_Adv + cl32_45_21_AdvXComp +
clm6_36_m21_ME_Comp +
pds_sum_c + v_iq_c + p_iq_c +
age_years_bsl_c + recruitment_centre + all_handedness) +
m1 + m2 + m3 + m4 + m5,
data = d,
sample_prior = "yes",
# file_refit = "on_change",
prior = c(prior(normal(0, 3), class = Intercept),
prior(normal(0, 5), class = b)),
iter = 2500,
warmup = 500,
chains = 4,
seed = 5,
file = "~/Desktop/PhD/resilience-im-burt/brms-fits/mediation_audit"
)
hyp_aud <- hyp("audit_total_score_fu3", med_aud)
hyp_aud$hypothesis |>
select(Evid.Ratio, Estimate, Est.Error, contains("CI"), Hypothesis) |>
mutate(across(where(is.numeric), ~round(., 3))) |>
rmarkdown::paged_table()Table of Bayesian hypothesis test results. (Evidence ratio > 1 supports “null” hypothesis. Evidence ratio < 1 supports “alternative” hypothesis.) Each row represents a different indirect effect for each unique pair of class and brain region.
Plotted below are the posteriors of the indirect effect.
med_aud |>
as_draws_df() |>
select(.draw,
contains("_class"),
contains("b_audittotalscorefu3_c")) |>
pivot_longer(cols = matches("(b_cl.*)_(class.*)"),
names_to = c("mediator_a", "class"),
names_pattern = "(b_cl.*)_(class.*)",
values_to = "a") |>
pivot_longer(cols = matches("(b_audittotalscorefu3)_(cl..)_(.*)"),
names_to = c("outcome", "mediator_b"),
names_pattern = "(b_audittotalscorefu3)_(cl.*)",
values_to = "b") |>
# compute ab for every class, for every brain mediator
mutate(ab = a * b,
mediator_a = str_remove(mediator_a, "b_"),
mediator_b = str_remove_all(mediator_a, "_"),
mediator = mediator_a == mediator_b) |>
#group_by(mediator_a) |>
#mean_qi(ab) |>
# mutate(across(where(is.numeric), ~round(.x, 3)))
ggplot(aes(x = ab, y = mediator_a)) +
stat_halfeye() +
xlim(-0.3, 0.3) +
labs(y = "", x = "a * b")
med_rap <- brm(
formula = bf(rapi_c_sum_fu3 ~ class + sex +
cl14_14_70_AdvXComp + cl20_44_40_ME_adv +
cl32_44_27_ME_Adv + cl32_45_21_AdvXComp +
clm6_36_m21_ME_Comp +
pds_sum_c + v_iq_c + p_iq_c +
age_years_bsl_c + recruitment_centre + all_handedness) +
m1 + m2 + m3 + m4 + m5,
data = d,
sample_prior = "yes",
# file_refit = "on_change",
prior = c(prior(normal(0, 3), class = Intercept),
prior(normal(0, 5), class = b)),
iter = 2500,
warmup = 500,
chains = 4,
seed = 5,
file = "~/Desktop/PhD/resilience-im-burt/brms-fits/mediation_rapi"
)
hyp_rap <- hyp("rapi_c_sum_fu3", med_rap)
hyp_rap$hypothesis |>
select(Evid.Ratio, Estimate, Est.Error, contains("CI"), Hypothesis) |>
mutate(across(where(is.numeric), ~round(., 3))) |>
rmarkdown::paged_table()Table of Bayesian hypothesis test results. (Evidence ratio > 1 supports “null” hypothesis. Evidence ratio < 1 supports “alternative” hypothesis.) Each row represents a different indirect effect for each unique pair of class and brain region.
Plotted below are the posteriors of the indirect effect.
med_rap |>
as_draws_df() |>
select(.draw,
contains("_class"),
contains("b_rapicsumfu3_c")) |>
pivot_longer(cols = matches("(b_cl.*)_(class.*)"),
names_to = c("mediator_a", "class"),
names_pattern = "(b_cl.*)_(class.*)",
values_to = "a") |>
pivot_longer(cols = matches("(b_rapicsumfu3)_(cl..)_(.*)"),
names_to = c("outcome", "mediator_b"),
names_pattern = "(b_rapicsumfu3)_(cl.*)",
values_to = "b") |>
# compute ab for every class, for every brain mediator
mutate(ab = a * b,
mediator_a = str_remove(mediator_a, "b_"),
mediator_b = str_remove_all(mediator_a, "_"),
mediator = mediator_a == mediator_b) |>
#group_by(mediator_a) |>
#mean_qi(ab) |>
# mutate(across(where(is.numeric), ~round(.x, 3)))
ggplot(aes(x = ab, y = mediator_a)) +
stat_halfeye() +
xlim(-0.3, 0.3) +
labs(y = "", x = "a * b")
med_pss <- brm(
formula = bf(pss_c_sum_fu3 ~ class + sex +
cl14_14_70_AdvXComp + cl20_44_40_ME_adv +
cl32_44_27_ME_Adv + cl32_45_21_AdvXComp +
clm6_36_m21_ME_Comp +
pds_sum_c + v_iq_c + p_iq_c +
age_years_bsl_c + recruitment_centre + all_handedness) +
m1 + m2 + m3 + m4 + m5,
data = d,
sample_prior = "yes",
# file_refit = "on_change",
prior = c(prior(normal(0, 3), class = Intercept),
prior(normal(0, 5), class = b)),
iter = 2500,
warmup = 500,
chains = 4,
seed = 5,
file = "~/Desktop/PhD/resilience-im-burt/brms-fits/mediation_pss"
)
hyp_pss <- hyp("pss_c_sum_fu3", med_pss)
hyp_pss$hypothesis |>
select(Evid.Ratio, Estimate, Est.Error, contains("CI"), Hypothesis) |>
mutate(across(where(is.numeric), ~round(., 3))) |>
rmarkdown::paged_table()Table of Bayesian hypothesis test results. (Evidence ratio > 1 supports “null” hypothesis. Evidence ratio < 1 supports “alternative” hypothesis.) Each row represents a different indirect effect for each unique pair of class and brain region.
Plotted below are the posteriors of the indirect effect.
med_pss |>
as_draws_df() |>
select(.draw,
contains("_class"),
contains("b_psscsumfu3_c")) |>
pivot_longer(cols = matches("(b_cl.*)_(class.*)"),
names_to = c("mediator_a", "class"),
names_pattern = "(b_cl.*)_(class.*)",
values_to = "a") |>
pivot_longer(cols = matches("(b_psscsumfu3)_(cl..)_(.*)"),
names_to = c("outcome", "mediator_b"),
names_pattern = "(b_psscsumfu3)_(cl.*)",
values_to = "b") |>
# compute ab for every class, for every brain mediator
mutate(ab = a * b,
mediator_a = str_remove(mediator_a, "b_"),
mediator_b = str_remove_all(mediator_a, "_"),
mediator = mediator_a == mediator_b) |>
#group_by(mediator_a) |>
#mean_qi(ab) |>
# mutate(across(where(is.numeric), ~round(.x, 3)))
ggplot(aes(x = ab, y = mediator_a)) +
stat_halfeye() +
xlim(-0.3, 0.3) +
labs(y = "", x = "a * b")
The results of this project suggest that early competence, as measured in adolescence, interacts with lifetime adversity in such a way as to be predictive of future mental health outcomes. This is aligned with conclusions by (Roisman et al. 2004), where they find that salient developmental tasks are predictive of future success within and across domains of competence, broadly defined. The findings in this study also corroborate with (Fritz et al. 2018) in that sub-domains of competence as defined here may serve to buffer the effects of adversity on mental health.
Regarding drug use, the results are null regarding the question at hand. What we want to know is if competence offsets the effects of adversity. Hence, the contrasts we care about are maladaptive-competent, and maladaptive-resilient since it’s expected that the competent and resilient groups have similar outcomes due to the effect of high competence, while the maladaptive group is high in adversity but low in competence.
We don’t see that effect with these contrasts on the AUDIT or RAPI scale since a significant portion of their posterior distributions overlap an effect of \(0\). Additionally, the differences are small in comparison to the magnitude of the differences on the mental health measures, the posteriors of which are more definitively well outside of a null effect.
The results for cigarette use and marijuana/hash use are more difficult to interpret since I have used the ordered probit model. For cigarette use, the contrast plot of coefficients suggest that the maladaptive and competent group differ in mean response on the latent distribution scale. We see that they also differ in expected value on the scale of the response. So it seems that competence does interact with adversity in a way as to suggest that the maladaptive group is more likely to smoke cigarettes than the competent group, on average. Additionally, a similar conclusion can be drawn for the vulnerable group relative to the competent group. However, it doesn’t seem that competence operates as a buffer to adversity since we care about the contrast between the maladaptive and competent group, and maladaptive and resilient group. A similar conclusion is drawn regarding marijuana/hash use.
With regard to the mediation analysis, none of the structural brain differences identified between the groups at age 14 mediated the effect of the competence/adversity groupings on future mental health or drug use. This is made clear by the fact that the posterior distributions of the indirect effects for every outcome are narrowly centered at zero. That is, the model is quite confident in saying that we have null effects.
| Characteristic | Overall, N = 2,1071 | competent, N = 7401 | resilient, N = 1461 | vulnerable, N = 9641 | maladaptive, N = 2571 |
|---|---|---|---|---|---|
| Sex | |||||
| Female | 1,075 (51%) | 376 (51%) | 91 (62%) | 452 (47%) | 156 (61%) |
| Male | 1,032 (49%) | 364 (49%) | 55 (38%) | 512 (53%) | 101 (39%) |
| Handedness | |||||
| Left | 196 (11%) | 67 (10%) | 15 (11%) | 87 (11%) | 27 (12%) |
| Right | 1,625 (89%) | 579 (90%) | 117 (89%) | 723 (89%) | 206 (88%) |
| Puberty score | 10.00 (8.00, 11.00) | 10.00 (7.00, 11.00) | 10.00 (8.00, 11.00) | 9.00 (7.00, 10.00) | 10.00 (8.00, 11.00) |
| Site | |||||
| 1 | 344 (16%) | 121 (16%) | 32 (22%) | 145 (15%) | 46 (18%) |
| 2 | 255 (12%) | 86 (12%) | 22 (15%) | 114 (12%) | 33 (13%) |
| 3 | 259 (12%) | 89 (12%) | 3 (2.1%) | 149 (15%) | 18 (7.0%) |
| 4 | 257 (12%) | 87 (12%) | 13 (8.9%) | 114 (12%) | 43 (17%) |
| 5 | 260 (12%) | 96 (13%) | 22 (15%) | 106 (11%) | 36 (14%) |
| 6 | 253 (12%) | 94 (13%) | 25 (17%) | 104 (11%) | 30 (12%) |
| 7 | 257 (12%) | 93 (13%) | 19 (13%) | 115 (12%) | 30 (12%) |
| 8 | 222 (11%) | 74 (10%) | 10 (6.8%) | 117 (12%) | 21 (8.2%) |
| Age (years) | 14.42 (14.14, 14.74) | 14.39 (14.12, 14.69) | 14.48 (14.18, 14.79) | 14.43 (14.14, 14.74) | 14.47 (14.16, 14.81) |
| Performance IQ | 78 (70, 85) | 81 (72, 87) | 79 (71, 85) | 77 (68, 84) | 77 (66, 84) |
| Verbal IQ | 81 (72, 89) | 83 (75, 90) | 82 (75, 90) | 79 (69, 88) | 80 (71, 89) |
| 1 n (%); Median (IQR) | |||||
| Variable | TDS | Internalizing | Externalizing | |||
|---|---|---|---|---|---|---|
| Beta | 95% CI1 | Beta | 95% CI1 | Beta | 95% CI1 | |
| class | ||||||
| competent | — | — | — | — | — | — |
| resilient | 0.07 | -0.16, 0.29 | 0.10 | -0.12, 0.32 | 0.01 | -0.22, 0.24 |
| vulnerable | 0.40 | 0.28, 0.53 | 0.40 | 0.28, 0.52 | 0.26 | 0.13, 0.39 |
| maladaptive | 0.76 | 0.57, 0.96 | 0.71 | 0.52, 0.90 | 0.57 | 0.38, 0.77 |
| sex | ||||||
| sexMale | -0.20 | -0.35, -0.06 | -0.44 | -0.58, -0.30 | 0.14 | -0.01, 0.29 |
| pds_sum_c | 0.00 | -0.04, 0.04 | 0.00 | -0.03, 0.04 | 0.00 | -0.04, 0.03 |
| v_iq_c | 0.00 | -0.01, 0.00 | 0.00 | 0.00, 0.01 | -0.01 | -0.01, 0.00 |
| p_iq_c | 0.00 | -0.01, 0.00 | 0.00 | -0.01, 0.00 | 0.00 | -0.01, 0.00 |
| age_years_bsl_c | 0.03 | -0.12, 0.18 | 0.02 | -0.13, 0.17 | 0.03 | -0.13, 0.19 |
| recruitment_centre | ||||||
| 1 | — | — | — | — | — | — |
| 2 | -0.20 | -0.42, 0.03 | -0.06 | -0.28, 0.16 | -0.27 | -0.50, -0.04 |
| 3 | -0.07 | -0.30, 0.16 | -0.13 | -0.35, 0.10 | 0.01 | -0.23, 0.24 |
| 4 | -0.23 | -0.46, 0.00 | -0.26 | -0.48, -0.03 | -0.10 | -0.34, 0.14 |
| 5 | -0.27 | -0.50, -0.05 | -0.21 | -0.44, 0.01 | -0.24 | -0.47, -0.01 |
| 6 | -0.09 | -0.32, 0.12 | -0.10 | -0.32, 0.12 | -0.06 | -0.29, 0.17 |
| 7 | -0.21 | -0.44, 0.01 | -0.17 | -0.39, 0.06 | -0.19 | -0.43, 0.05 |
| 8 | 0.04 | -0.22, 0.31 | -0.04 | -0.30, 0.21 | 0.13 | -0.13, 0.38 |
| all_handedness | ||||||
| all_handednessRight | 0.10 | -0.08, 0.28 | 0.10 | -0.07, 0.27 | 0.05 | -0.14, 0.24 |
| 1 CI = Credible Interval | ||||||
| Variable | CESD score | PSS score | ||
|---|---|---|---|---|
| Beta | 95% CI1 | Beta | 95% CI1 | |
| class | ||||
| competent | — | — | — | — |
| resilient | 0.03 | -0.14, 0.22 | 0.02 | -0.20, 0.25 |
| vulnerable | 0.18 | 0.07, 0.29 | 0.24 | 0.12, 0.37 |
| maladaptive | 0.48 | 0.30, 0.66 | 0.54 | 0.34, 0.73 |
| sex | ||||
| sexMale | -0.15 | -0.27, -0.03 | -0.25 | -0.40, -0.10 |
| pds_sum_c | -0.01 | -0.04, 0.02 | -0.01 | -0.05, 0.03 |
| v_iq_c | 0.00 | -0.01, 0.00 | 0.00 | -0.01, 0.00 |
| p_iq_c | -0.01 | -0.01, 0.00 | -0.01 | -0.01, 0.00 |
| age_years_bsl_c | 0.07 | -0.06, 0.20 | 0.13 | -0.03, 0.27 |
| recruitment_centre | ||||
| 1 | — | — | — | — |
| 2 | -0.20 | -0.40, 0.00 | -0.39 | -0.62, -0.15 |
| 3 | -0.15 | -0.36, 0.06 | -0.36 | -0.59, -0.13 |
| 4 | -0.03 | -0.23, 0.17 | -0.22 | -0.46, 0.02 |
| 5 | -0.02 | -0.22, 0.17 | -0.21 | -0.43, 0.02 |
| 6 | -0.06 | -0.26, 0.14 | -0.17 | -0.40, 0.06 |
| 7 | -0.12 | -0.32, 0.09 | -0.13 | -0.37, 0.11 |
| 8 | -0.14 | -0.37, 0.08 | -0.15 | -0.40, 0.11 |
| all_handedness | ||||
| all_handednessRight | 0.00 | -0.15, 0.16 | 0.02 | -0.17, 0.19 |
| 1 CI = Credible Interval | ||||
| Variable | AUDIT score | RAPI score | ||
|---|---|---|---|---|
| Beta | 95% CI1 | Beta | 95% CI1 | |
| class | ||||
| competent | — | — | — | — |
| resilient | 0.05 | -0.14, 0.24 | 0.05 | -0.04, 0.14 |
| vulnerable | -0.03 | -0.14, 0.07 | 0.01 | -0.04, 0.06 |
| maladaptive | 0.13 | -0.04, 0.29 | 0.03 | -0.05, 0.12 |
| sex | ||||
| sexMale | 0.31 | 0.19, 0.44 | 0.05 | -0.01, 0.11 |
| pds_sum_c | -0.01 | -0.04, 0.02 | -0.01 | -0.02, 0.01 |
| v_iq_c | 0.00 | 0.00, 0.01 | 0.00 | 0.00, 0.00 |
| p_iq_c | 0.00 | 0.00, 0.01 | 0.00 | 0.00, 0.00 |
| age_years_bsl_c | -0.06 | -0.19, 0.06 | 0.01 | -0.05, 0.07 |
| recruitment_centre | ||||
| 1 | — | — | — | — |
| 2 | -0.45 | -0.63, -0.27 | -0.09 | -0.17, -0.01 |
| 3 | -0.33 | -0.52, -0.15 | -0.06 | -0.14, 0.03 |
| 4 | -0.36 | -0.55, -0.16 | -0.06 | -0.15, 0.02 |
| 5 | -0.40 | -0.58, -0.21 | -0.03 | -0.12, 0.05 |
| 6 | 0.01 | -0.18, 0.20 | 0.07 | -0.02, 0.17 |
| 7 | -0.31 | -0.50, -0.12 | 0.07 | -0.03, 0.16 |
| 8 | 0.27 | 0.05, 0.49 | 0.23 | 0.09, 0.37 |
| all_handedness | ||||
| all_handednessRight | 0.04 | -0.11, 0.19 | 0.01 | -0.06, 0.08 |
| 1 CI = Credible Interval | ||||
| Variable | Cigarette Use | Marijuana/Hash Use | ||
|---|---|---|---|---|
| Beta | 95% CI1 | Beta | 95% CI1 | |
| (Intercept)[1] | 0.15 | -0.18, 0.47 | -0.78 | -1.3, -0.32 |
| (Intercept)[2] | 0.43 | 0.11, 0.75 | -0.11 | -0.58, 0.35 |
| (Intercept)[3] | 0.76 | 0.44, 1.1 | 0.16 | -0.31, 0.63 |
| (Intercept)[4] | 1.1 | 0.79, 1.5 | 0.49 | 0.01, 0.95 |
| (Intercept)[5] | 1.7 | 1.4, 2.0 | 0.79 | 0.32, 1.3 |
| (Intercept)[6] | 2.6 | 2.2, 3.0 | 1.1 | 0.67, 1.6 |
| classresilient | 0.21 | -0.09, 0.50 | 0.11 | -0.31, 0.55 |
| classvulnerable | 0.23 | 0.05, 0.40 | 0.27 | 0.00, 0.53 |
| classmaladaptive | 0.32 | 0.07, 0.57 | 0.30 | -0.05, 0.65 |
| pds_sum_c | -0.06 | -0.10, -0.02 | -0.06 | -0.12, 0.00 |
| v_iq_c | 0.00 | -0.01, 0.00 | 0.00 | -0.01, 0.01 |
| p_iq_c | -0.01 | -0.01, 0.00 | 0.00 | -0.01, 0.01 |
| age_years_bsl_c | 0.08 | -0.13, 0.28 | 0.11 | -0.20, 0.43 |
| recruitment_centre2 | 0.21 | -0.10, 0.51 | -0.25 | -0.70, 0.22 |
| recruitment_centre3 | -0.04 | -0.35, 0.26 | -0.09 | -0.53, 0.36 |
| recruitment_centre4 | 0.46 | 0.16, 0.75 | 0.06 | -0.37, 0.48 |
| recruitment_centre5 | -0.11 | -0.41, 0.19 | -0.22 | -0.67, 0.21 |
| recruitment_centre6 | -0.11 | -0.41, 0.19 | -0.19 | -0.63, 0.26 |
| recruitment_centre7 | 0.03 | -0.27, 0.33 | 0.07 | -0.40, 0.55 |
| recruitment_centre8 | -0.09 | -0.42, 0.24 | -0.60 | -1.1, -0.14 |
| all_handednessRight | 0.01 | -0.23, 0.26 | -0.16 | -0.52, 0.19 |
| 1 CI = Credible Interval | ||||